DEMATEL(decision making trial and evaluation laboratory,决策实验分析法)[19]151-162方法是针对于复杂系统,研究其中复杂因素的逻辑关系,通过计算影响度、被影响度、中心度和原因度四个数量特征,定量分析各个风险因素的重要程度和属性,进而确定关键风险因素。该方法能够反映各个风险因素之间的影响强度,但不能明确各个风险因素的层次结构。为解决此弊端,引入ISM模型。ISM(interpretive structure modeling,解释结构模型法)方法以定性分析为主,定性定量分析相结合,主要是分析系统因素相互关联关系及相互关系变化时对系统总体的影响,通过建立邻接矩阵,求解可达矩阵,最后构造系统因素相互影响的递阶层次结构模型,但它不能定量地表示各风险因素之间的相互影响关系。DEMATEL和ISM两种方法存在共性,又能相互取长补短,将DEMATEL和ISM相互融合,既明确系统风险因素间相互影响程度又能建立系统风险因素的递阶层次结构模型,具有更完备的解释功能。集成DEMATEL-ISM模型构建思路如图1。
3.1 构建直接关系矩阵
通过对PPP项目具有5年以上研究经验的大学教授和PPP项目管理咨询公司的中专业人士及海绵城市领域研究人员发放问卷进行打分的形式,采用0~5记分法,判断每个因素的重要性。问卷填写如表2所示。
将收集到10位资深权威专家打分,采用算数标准平均法对数据处理后可得初始直接关系矩阵M如下:

其中,因子i对因子j的影响表示为aij,如果风险因素i不直接影响风险因素j,记为0分,其余的1、2、3、4、5分别表示影响非常小、影响较小、影响中等、影响较大、影响大。
3.2 求标准矩阵Z和总关系矩阵T
把直接关系矩阵M标准化得到标准矩阵Z。规范化公式为:
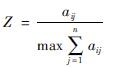 (1)
(1)
求出总关系矩阵T,公式如下:

式中,E是单位矩阵,(E-Z)-1是(E-Z)的逆矩阵。
文中所有矩阵计算结果均由MATLAB软件编写程序代码计算得出。由于篇幅原因,只列出最终的T矩阵,如下:

3.3 “四度计算”
由总关系矩阵中的tij可以进一步求出每一个因素的影响度D、被影响度C、中心度M和原因度N。tij表示因素i对因素j所产生的直接影响加上间接影响的程度,即因素i对因素j产生的综合影响程度。在总关系矩阵T中,“影响度di”是行的和,“被影响度ci”表示列的和。公式如下:
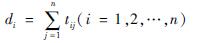 (3)
(3)
 (4)
(4)
“中心度d+c”,影响度和被影响度相加,表示各因素之间的关系; “原因度d-c”是对其他因素的影响。公式如下:
Mi=di+ci(5)
Ni=di-ci(6)
各风险因素的“四度”值,如表3所示。
下一步,基于原因度和中心度绘制散点图。根据各因素的成因程度,以风险因素的中心度为横坐标,原因度为纵坐标,绘制各个因素的原因-结果图,确定关键风险因素(图2)。
3.4 确定整体影响矩阵
综合影响矩阵反映的不同因素之间的影响关系和影响程度,其中弊端是不能反映出对本身因素的影响。因此需要计算反映系统因素整体影响关系的矩阵,即整体影响矩阵H。公式如下:
H=T+I=hj(7)
式中,I为单位矩阵。
3.5 确定可达阵
确定整体影响矩阵后,可进一步计算可达矩阵K,K=|kij|如下:
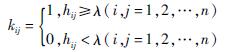 (8)
(8)
式中,λ为阈值,阈值的大小根据实际情况进行科学的设定,阈值λ的设定主要为了舍掉影响程度较小的影响关系。λ的取值越大,对系统结构简化越明显,但在可达阵区域划分时,容易形成两个以上的连通域,这时就需要重新研究因素之间的相互影响关系。kij为节点i到节点j的关联值,kij=1表明两个节点关联。经过多次测算取阈值λ=α+β=0.157 8,其中α为综合影响矩阵T的平均数,β为T的标准差,由此构建可达矩阵K,如下:

3.6 确定各风险因素的可达集和前因集
根据可达矩阵K,可计算出每个风险因子的可达集P(Bi)与前因集Q(Bi)。可达集P(Bi)为因素Bi可以直接到达的因素集合,即可达矩阵K中第i行因素为1 的列对应的因素构成; 前因集Q(Bi)是由可达阵K中第i列因素为1的行对应的因素构成,是可以到达因素Bi的全部因素集合。公式如下:
P(Bi)={Bj∈Bkij=1}(9)
Q(Bi)={Bi∈Bkji=1}(10)
C={Bi∈BP∩Q=P}(11)
式中,C为共同集合且C中包括了n个级别因素集。在可达矩阵K中,按照顺序依次划去共同集合C中每级因素对应的行和列,一直重复这个步骤,既能得到C的各层级因素,与此同时,可达矩阵中所有因素也已被划除。
3.7 解释结构模型建立
重复2.6中的式(9)、式(10)和式(11),直到所有的因素被划除,根据划除因素的顺序,可得表4,并绘制因素递阶层次结构图(图3)。图3中数字节点代表的是建设海绵城市复杂系统中的各风险因素,各因素之间的影响关系用有向箭头“→”表示。
图3 PPP模式下SC风险影响因素递阶层次结构模型
3 结果分析
运用集成DEMATEL-ISM方法对PPP模式下海绵城市风险影响因素研究分析时,首先运用DEMATEL方法确定海绵城市风险影响因素两两之间的直接影响关系; 然后进一步计算综合影响矩阵,再加上相应的单位矩阵,得到整体影响矩阵; 通过合理设置阈值,得到ISM方法需要的可达矩阵; 最后经过运算,得到PPP模式下海绵城市风险影响因素的6级结构模型。DEMATEL方法计算的中心度可以反映风险因素的相对重要程度,据算出的原因度可以明确各因素之间的因果关系; ISM方法得出的结构模型则可以直观地观察出各因素间相互关联关系。
3.1 “四度”结果分析
通过对PPP模式下SC风险因素的影响度、被影响度、中心度、原因度分析(表1),可看出,7个风险因素被确定为正值的原因度(D-C=N),被称为原因因素。说明原因因素对其他因素的影响比其他因素对自身的影响更加显著,包括B1政策法律不完善、B2政府信用风险、B4SC专业经验不足、B10技术缺陷、B13不可抗力风险、B14政府腐败风险、B15市场需求变化。举例来说,对于政策法律不完善因素,由国家制定,它是受国家政策影响,不受其他因素(如技术缺陷、管道改造困难、进度延误等)直接影响,却能够直接影响其他因素; 立法是一切活动的基本,若海绵城市建设缺乏法律政策保障,社会资本投入的风险性、不确定程度也会变高,不利于吸引外资,因此,完善的法律体系有助于海绵城市建设资金的征集。对于民众反对因素,是由人民意志决定的,也不受其他因素直接影响。通过改进原因因素,可间接改善结果因素,从而逐渐减弱整个系统的风险程度。
其余9个风险因素具有负值原因度(D-C=N),被称为结果因素,包括B3融资风险、B5规划设计变更、B6招标风险、B7政府腐败风险、B8工期延误、B9成本超支、B11施工安全隐患、B12管道改造风险、B16营业收益不足,说明这些因素对其他因素的影响小于其他因素对自身的影响,具有较强的依赖性,且多数位于递阶层次结构模型的中上层,是风险因素系统的最终目标。
中心度(D+C=M)表示风险因素在整个分析系统中的重要程度,16个风险因素的突出重要程度从大到小依次是B3融资风险>B9成本超支>B16营业收益不足>B8工期延误>B5规划设计变更>B12管道改造困难>B2政府信用风险>B11施工安全隐患>B10施工技术缺陷>B4 SC专业经验不足>B15市场需求变化>B6招标风险>B7项目唯一性风险>B14政府腐败风险>B13不可抗力风险>B1政策法律不完善。通过风险因素中心度排序可知进度延误、成本超支、营业收益不足、施工技术缺陷在风险系统中的重要性突出,对于PPP模式下海绵城市项目风险影响较大。若要保证项目成功顺利运行收益,降低风险发生的概率,应重点考虑以上这些风险因素。结合图2可知,B2政府信用风险、B8工期延误、B9成本超支、B16营业收益不足是海绵城市风险关键因素,同时符合政策法律不完善、不可抗力风险、运维能力不足会导致进度延误、成本超支风险发生的工程实际情况。由此可见,充足的资金和强硬的技术实力对削弱海绵城市建设风险的重要性不容忽视。
3.2 递阶层次结构模型分析
PPP模式下海绵城市风险影响因素的递阶层次结构模型,形象直观地反映了风险因素之间的相互影响关系和层次结构,这是ISM建模的优势。发出箭头多的风险因素与表2中影响度D较大值的风险因素相对应,表明该风险因素影响其他风险因素的程度大于被其他风险因素影响的程度,决策者在提出风险管理措施时,应着重考虑此类风险因素; 被指向箭头多的风险因素与表2中被影响度C的较大值的因素相对应,表明该风险因素影响其他风险因素的程度小于被其他风险因素影响的程度,通过观察这些风险因素的发生率能间接说明风险管理措施的实施效果。位于顶层L1和L2层的B6招标风险、B11施工安全隐患、B10施工技术缺陷、B16营业收益不足、B8进度延误、B9成本超支等是影响PPP模式下海绵城市风险的直接影响层,也是系统风险管理的最终目标,地位重要; 位于L3和L4层级的B3融资风险、B4SC专业经验不足、B5规划设计变更、B12管道改造困难、B13不可抗力风险,这些风险因素的影响度和被影响度都处于比较靠前的位置,受其他因素影响大也易影响其他因素,属于过渡层级风险因素,起到承上启下的作用,地位关键; 处于底层L5、L6和L7层级的B14政府腐败风险、B15市场需求变化、B2政府信用风险等政府因素是不易被其他风险因素影响且较易影响其他风险因素,起基础作用,最终通过L1、L2、L3层级的因素对PPP模式下海绵城市风险产生直接影响。
融资风险、政府信用风险、工期延误、成本超支、营业收益不足等重要风险因素都集中在建设施工阶段和运营维护阶段,同样符合工程实际情况,对于项目建设施工阶段和运营维护阶段安全工作应给予重点关注。