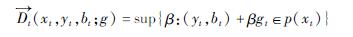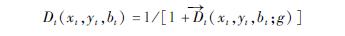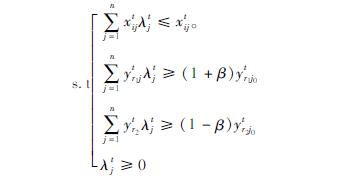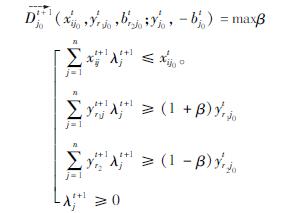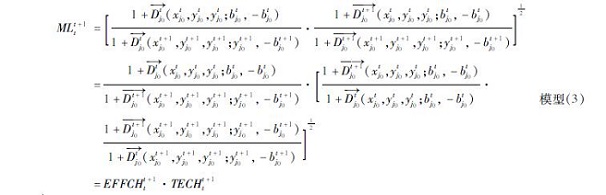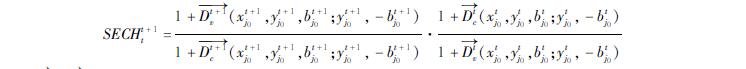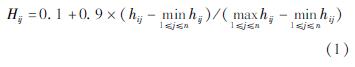(1)超效率SBM模型(Super-SBM模型)。Super-SBM模型即超效率SBM模型是Tone^[18]在SBM模型基础之上创新提出的,此模型能够对用SBM模型测算得出有效决策单元进行第二次测算和排序。主要分为两步:第一步是基于SBM模型对所有决策单元的相对效率进行测度; 第二步,针对有效决策单元运用Super-SBM模型开展进一步估算。本文假设江苏省整个工业经济活动系统中共有 个独立的决策单元(此处把江苏省下辖的13个地级视为13个独立的决策单元)即称DMU_j,j=1,2,3…n; n=13),每个工业决策单元中有m种工业投入x_i,i=1,2,3…m,有q₁种工业期望产出y^g_r,r=1,2,3,…,q₁,有q₂种工业非期望产出y^b_t,t=1,2,3…q₂。模型构建时定义工业投入矩阵X=[x₁,x₂,x₃,…,x_n]∈R^m×n,工业期望产出矩阵Y^g=[y^g₁,y^g₂,y^g₃,…,y^g_n]∈R^q₁×n,工业非期望产出矩阵,Y^b=[y^b₁,y^b₂,y^b₃,…,y^b_n]∈R^q₂×b。s^-_i,s^g+_r,s^b-_t分别表示江苏省工业经济活动投入松弛、期望产出松弛和非期望产出松弛调整变量。包含非期望产出的生产可能性集合则可以表示为P={(x,y^g,y^b)|x≥Xλ,y^g≤Y^gλ,y^b≥Y^bλ},其中λ为权重参数向量。考虑非期望产出y^b_t的SBM模型则可以用以下线性规划进行表达:

上述模型的最优解用ρ^*来进行表示,取值情况反映被评价决策单元的效率值大小,0<ρ^*<1,说明当前决策单元处于DEA无效状况,ρ^*=1,说明当前决策单元处于DEA有效状况。

在模型(1)测算结果的基础之上进一步使用Super-SBM模型对有效单元进行测算,考虑非期望产出的Super-SBM模型可以表示如下:

ρ^*_SE为此模型的最优解,ρ^*_SE≥1时,表明该决策单元为有效。本文联合运用模型(1)和模型(2)来测算江苏省工业经济发展效率水平。

(2)Malmquist-Luenberger(M-L)模型。首先定义一个包含非期望产出(非合意产出)的环境技术模型。假设江苏省各地区工业经济活动系统共有用m种工业活动要素投入x=(x₁,x₂,x₃,…,x_m)∈R⁺_m,q₁种工业期望产出y=(y₁,y₂,y₃,…,y_q1)∈R⁺_q1,q₂种非期望产出b=(b₁,b₂,b₃,…,b_q2)∈R⁺_q2。t时期的投入产出向量可以表示为(x_t,y_t,b_t),t期生产可能集可以表示为:

式中,λ_tj表示权重向量,若∑ⁿ_j=1λ_tj=1时,环境生产技术规模报酬可变,若0≤∑ⁿ_j=1λ_tj<λ_tj<1时,环境生产技术规模报酬不变。

可以在生产可能集合p_t(x_t)上定义方向距离函数,其表示为:

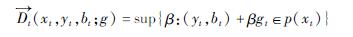
式中,g_t为t时期产出变化的方向向量,本文根据Chung等^[9]对g_t的设定,设定为g_t=(y_t,-b_t)表示期望产出的增加的方向以及非期望产出减少的方向。β表示某一决策单元沿着g_t=(y_t,-b_t)能够扩展的最大倍数,客观反映着当前决策单元实际产出与最佳前沿面的距离。β越小表明决策单元距离前沿越近,意味着效率越高,反之,效率水平越低。Shephard产出距离函数与方向性距离函数关系可以表示如下:

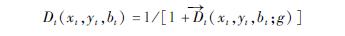
基于D^t_j0(x^t_tj0,y^t_r1,j0,b^t_r2,j0; y^t_j0,-b^t_j0)、D^t+1_j0(x^t+1_xj0,y^t+1_r1j0,b^t+1_r2j0; y^t+1_j0,-b^t+1_j0)、D^t+1_j0(x^t_ij0,y^t_r1j0,b^t_r2j0; y^t_j0,-b^t_j0)、D^t_j0(x^t+1_tj0,y^t+1_r1j0,b^t+1_r2j0; y^t+1_j0,-b^t+1_j0)四个距离函数来构造Malmquist-Luenberger(ML)生产率指数,进而来测算工业全要素生产率的变化。以上四个方向距离函数需要构造四个线性规划式进行分别求解。其中两个为t或t+1时期决策单元分别参考各自t或t+1时期的技术前沿水平。例如,假设第j₀个决策单元在t时期的投入与产出组合为(x_tj0,y_tj0,y_tj0),那么D^t_j0(x^t_xj0,y^t_r1j0,b^t_r2j0; y^t_j0,-b^t_j0)可以通过以下线性规划进行求解。

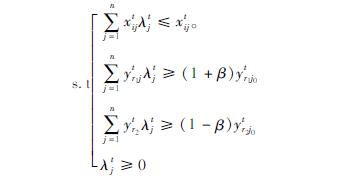
式中,i=1,2,3…,m,r₁=1,2,3,…q₁,r₂=1,2,3,…,q₂,t=1,2,3,…,T,λ^t_i≥0,表示在t时期横截面的观测值权重。

另外两个距离函数为混合距离函数,涉及跨期参比效率的问题,例如D^t+1_j0(x^t_ij0,y^t_r1j0,b^t_r2j0; y^t_j0,-b^t_j0)可以通过以下线性规划进行求解。

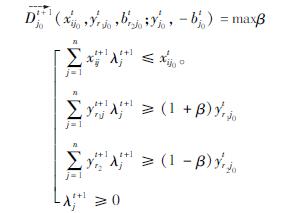
式中,λ^t+1_i≥0,表示在t+1时期横截面的观测值权重。

基于前面所构建的四个距离函数,第j₀个决策单元t到t+1时期的Malmquist-Luenberger指数:

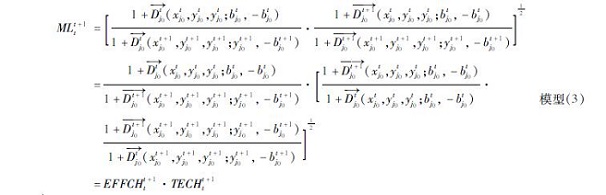
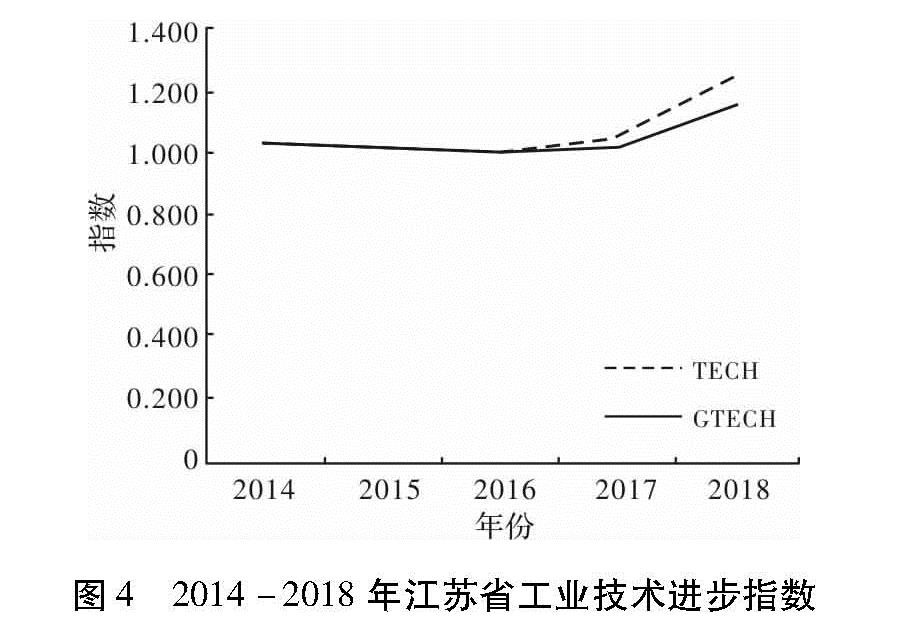
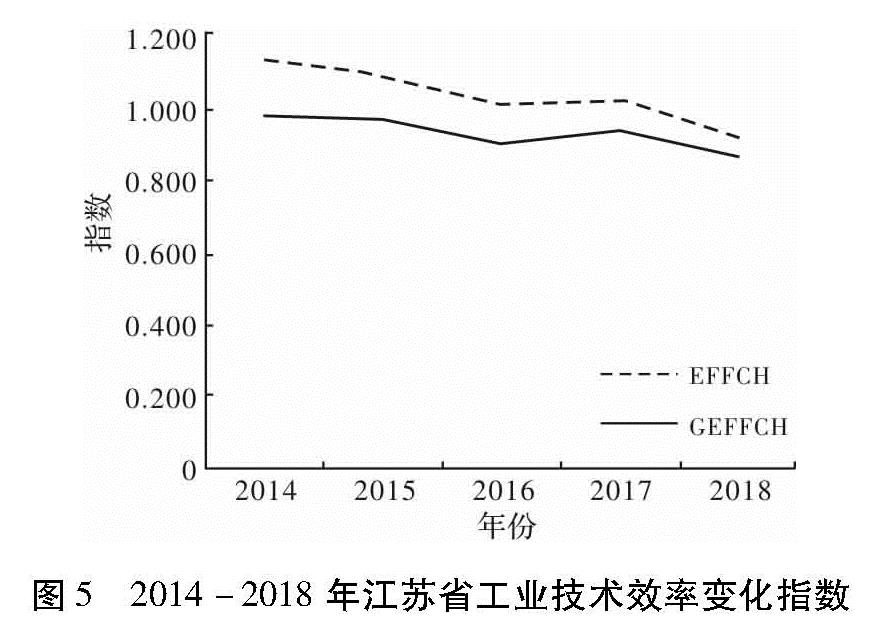
式中,D^t_j0^→(x^t_j0,y^t_j0,y^t_j0; b^t_j0,-b^t_j0),D^t+1_j0(x^t+1_j0,y^t+1_j0,y^t+1_j0; y^t+1_j0,-b^t+1_j0)分别表示t期和t+1期的方向距离函数; D^t_j0^→(x^t+1_j0,y^t+1_j0,y^t+1_j0; y^t+1_j0,-b^t+1_j0),D^t+1_j0^→(x^t_j0,y^t_j0,y^t_j0; b^t_j0,-b^t_j0)分别表示基于t期前沿技术的t+1期决策单元的混合距离函数以及基于t+1期前沿技术的t期决策单元的混合距离函数。ML^t+1_t在本文中表示从t到t+1时期江苏省工业全要素生产率变动指数。ML^t+1_t>1,表示江苏省工业全要素生产率进步,ML^t+1_t<1,表示江苏省工业全要素生产率下降。EFFCH^t+1_t在本文中表示从t到t+1时期江苏省工业技术效率变化指数,反映着江苏省整个工业前沿技术的整体变化情况,TECH^t+1_t>1表示整体工业技术进步,TECH^t+1_t<1表示整体工业技术衰退。EFFCH^t+1_t反映着决策单元距离其前沿面距离的变化情况,也反映着决策单元对前沿技术的追赶效应,反映决策单元对生产技术的利用情况,逼近“最佳实践者”的情况。EFFCH^t+1_t>1,表示决策单元从t到t+1期更加靠近当期技术前沿面,工业技术效率有所提升。EFFCH^t+1_t<1,表示决策单元从t到t+1期更加远离当期技术前沿面,工业技术效率有所下降。

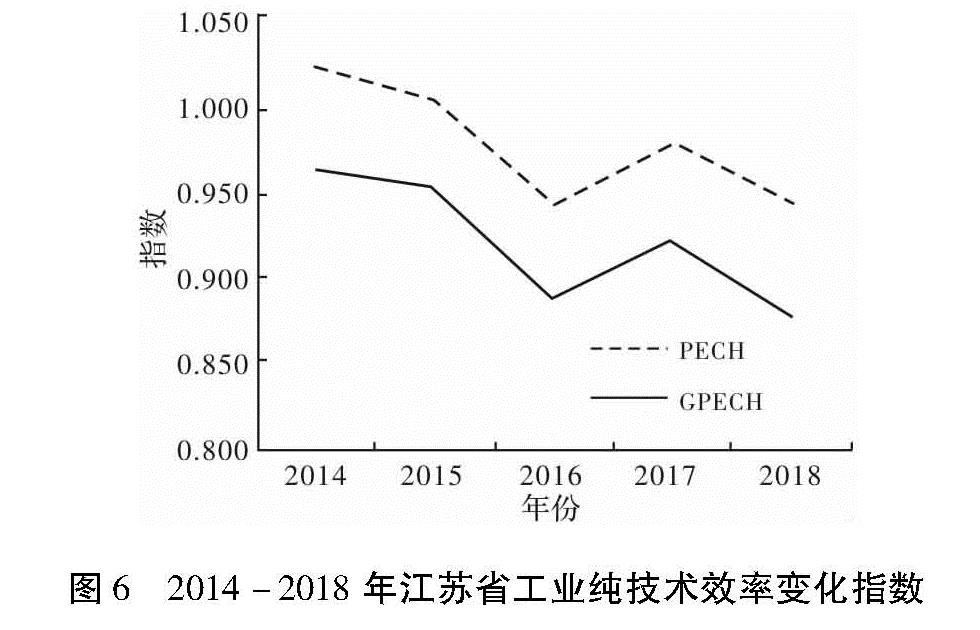
技术效率变动指数(EFFCH^t+1_t)能够分解为纯技术效率变动指数(PECH)和规模效率变化指数(SECH)两个变量。即,EFFCH^t+1_t=PECH^t+1_t·SECH^t+1_t,故有:

其中,

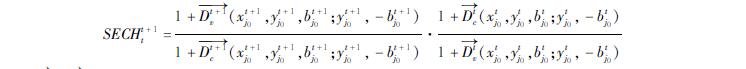
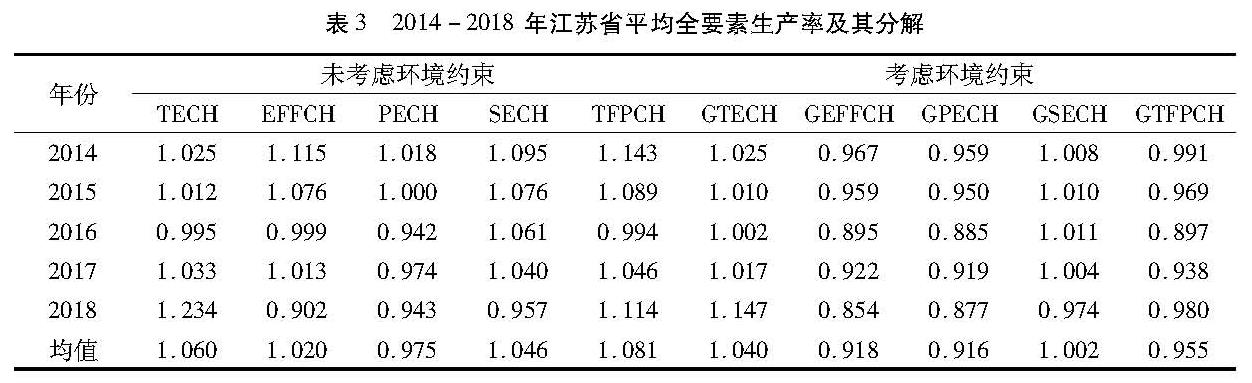
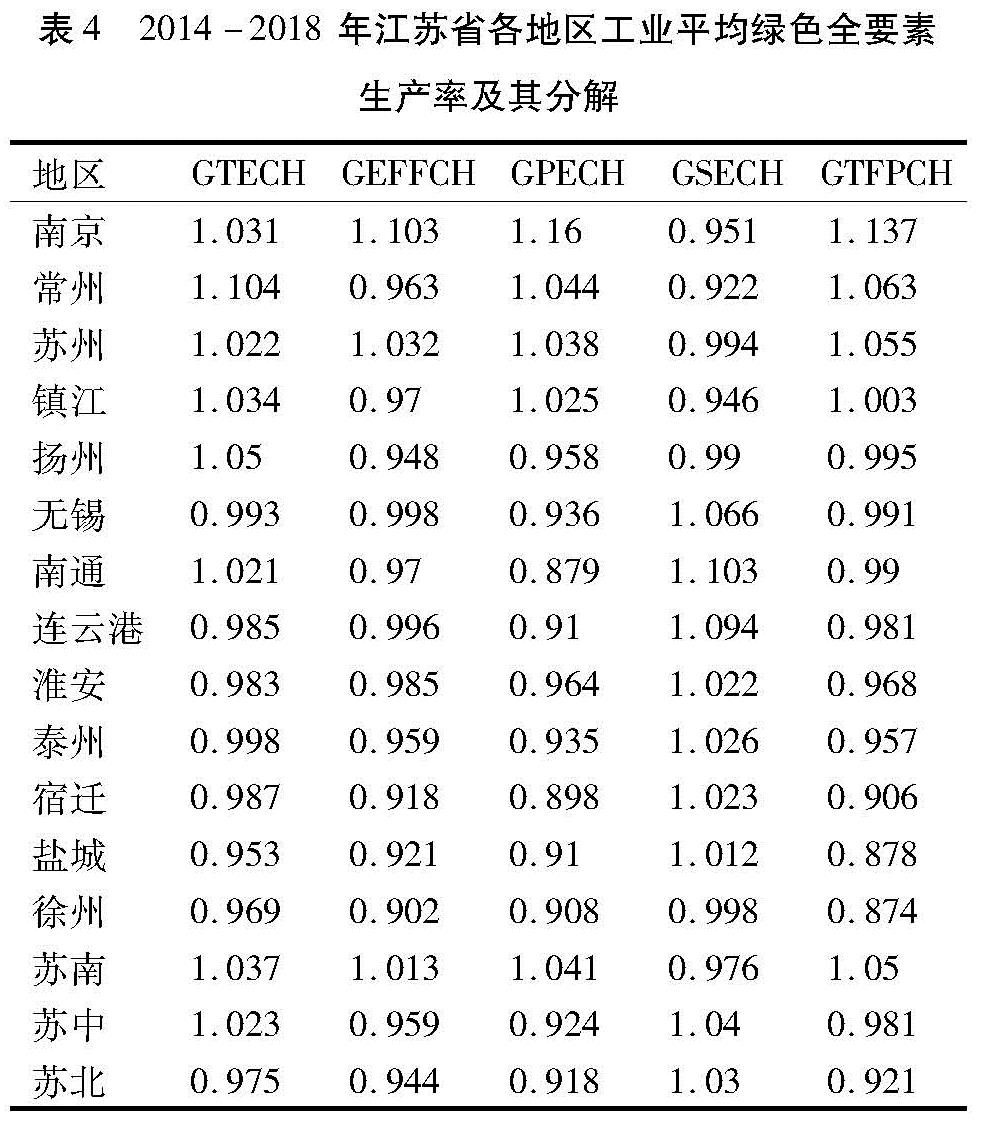
式中,D_v^→和D_c^→分别规模报酬可变和规模报酬不变条件下的方向性距离函数。SECH^t+1_t表示规模效应的变化情况。SECH^t+1_t>1,表示规模效应水平上升,SECH^t+1_t<1,表示规模效应水平下降。PECH^t+1_t表示纯技术效率水平的变化情况,PECH^t+1_t>1,表示纯技术效率水平提高,PECH^t+1_t<1,表示纯技术效率水平下降。考虑环境约束即非期望产出的工业全要素生产率及其分解指标,本文在对应的指标前加上前缀G以示区分。GTFPCH、GTECH、GEFFCH、GPECH、GSECH分别表示绿色(环境)全要素生产率的变化、绿色(环境)技术进步、绿色(环境)技术效率变化、绿色(环境)纯技术效率变化和绿色(环境)规模效率变化。

基于数据包络分析法对江苏省工业经济发展效率和全要素生产率变化进行测度与评价必须正确合理地确定工业经济活动投入与产出相关评价指标。参考学界以前相关研究成果同时考虑相关数据获取的可得性,主要从工业经济投入、工业经济期望产出和工业经济非期望产出三个方面综合确定江苏省工业经济活动评价指标。江苏省工业经济活动投入要素指标主要参考周五七 ^[15]、李苏苏等^[19]等学者研究成果,选取劳动力投入、资本投入和企业单位个数三个指标作为工业活动投入要素指标。其中劳动力投入采用规模以上工业全年平均从业人数来进行替代。工业活动资本投入采用借鉴赵春雨等^[20]的方法以工业固定资产净值来衡量,但是由于其无法完整获取,采用规模以上工业资产总额来替代工业固定资产净值。企业单位个数则采取规模以上工业企业单位个数。考虑环境约束的江苏省工业经济活动产出指标可以分为期望产出指标和非期望产出指标。以规模以上工业总产值作为工业活动期望产出指标,并根据工业产品出厂价格进行平减处理。参考谭涛^[21]以碳排放量作为环境约束的重要考量,纳入工业绿色效率的测算,以单位工业增加值碳排量作为非期望产出指标,主要是根据单位工业增加值能耗乘以标准煤碳排放系数值2.736^[22]得到。

以上规模以上工业企业相关指标数据均来自2013-2018年江苏省《统计年鉴》,并根据式(1)对各指标进行无量纲化处理,以确保基础指标数据的科学合理。

式中,min_1≤j≤nh_ij和max_1≤j≤nh_ij分别表示第i项指标的最小值与最大值。h_ij表示第j个决策单元第i项指标。经过转化之后的各指标H_ij∈[0.1,1]。

根据超效率SBM模型前述模型(1)和模型(2)运用MAXDEA8.0PRO软件测算对江苏省13个城市2013-2018年进行工业发展静态效率测算分析,具体测算结果如表1和表2所示。

表1 2013-2018年江苏省各市工业发展效率

表2 2013-2018年 江苏省各市工业绿色发展效率

图1 2013-2018年江苏省工业经济

图2 2013-2018年江苏省工业经济绿色发展效率均值

(1)由表1可知,不考虑非期望产出的2013-2018年江苏省工业经济发展效率大于1的有7个地区,依次是苏州、南京、连云港、常州、南通、淮安和镇江。其中,苏州的工业经济发展效率水平最高,均值为2.005,虽然2018年有所下降,但是整体上呈现上升趋势。这主要是与苏州市工业基础雄厚,交通十分便利,工业园区经济发展较好,工业总产值增长较快有较大关系。2014年来苏州市大力推动工业经济升级,努力培育苏州自主品牌,提升工业企业全员劳动生产率,重点推进战略新兴产业和高兴技术产业发展。其次是南京市,2013-2018年工业经济发展效率一直大于1,处于DEA相对有效,均值为1.319。南京工业发展基础夯实,政策优势明显,工业产业结构不断优化,产业集群效应显著,工业质量效益不断得以提高。扬州、宿迁、泰州、盐城、无锡和徐州地区2013-2018年工业经济发展效率均值小于1,尚未达到DEA有效,其中泰州、盐城和徐州3个地区2013-2018年一直处于DEA无效,其他地区工业发展效率值有所波动。徐州工业经济发展效率处于江苏省内最低水平,说明徐州作为传统资源型城市工业转型发展较为缓慢。推动徐州传统产业转型升级,振兴徐州工业基地仍然需要走很长一段路。

(2)从江苏省工业经济整体发展效率来看,2013-2018年工业发展效率均值为1.049,除了2018年工业经济发展效率为0.937,有所下降且未达到DEA有效,总体上来看工业发展效率较为平稳,达到了DEA相对有效。从表1和图1可以发现,江苏省三大区域工业发展效率差异十分明显,江苏省内区域工业经济发展不够平衡。苏南地区2013-2018年工业经济发展效率水平处于省内领先水平,各年效率值均大于1,6年均值为1.049,整体达到了DEA有效,这主要是由于苏南地区地理位置优越紧邻上海地区,依托长三角经济带,工业经济和科技发展水平较高。苏中地区工业经济发展效率次之,2015年以来不断处于下降,均值为0.943。苏北地区工业经济发展效率处于三大区域最低水平,2013-2018年苏北地区工业发展效率值都小于1,表明整体来看苏北地区工业发展效率未达到DEA有效,工业经济发展相对较为落后,因此必须进一步加大工业先进科技自主创新与研发,深入推进产业结构的深度优化与调整,促进苏北工业经济发展。

(3)由表2可知,江苏省2013-2018年工业绿色发展效率均值来看总体上呈现波动且略微下降的趋势,虽然从六年整体均值来看,江苏省工业绿色发展效率为1.020,达到了DEA相对有效,但是2016-2018年工业绿色发展效率值均都小于1,未达到DEA有效,说明江苏省工业绿色发展效率水平面临着下降的风险,因此需要强化工业绿色科技投入、研发与创新,进一步推动红色绿色转型发展。具体来说,苏州、南京、南通、连云港在工业发展效率和绿色发展效率都表现出较为明显的优势,而盐城虽然2013-2018年工业经济发展效率处于0.706～0.854,均值为0.789,未达到DEA有效,其省内效率排名第11位,较为靠后,但是其工业绿色发展效率值处于1.013～1.153,均值为1.068,达到了DEA有效,省内绿色效率排名第5位,说明盐城市在工业绿色集约发展和绿色制造方面工作成效较为明显。徐州、宿迁、泰州、无锡四个地区的工业绿色发展效率值排名靠后,这与其在未考虑非期望产出的工业经济发展效率排名情况大体一致,位于省内较低水平,说明这几个地区在推动工业规模经济增长的同时,需要更加关注节能减排与工业污染治理,推动工业经济绿色高质量发展。

(4)由表2和图2可以看出,江苏省三大区域仅有苏南地区工业绿色发展效率一直保持在1以上,均值为1.096,高于江苏省工业绿色发展效率均值1.020,表明苏南地区地区受到长三角经济带辐射效果明显,在降低工业能耗和污染治理、推动工业经济绿色转型发展方面表现出较为明显的优势。而苏中、苏北工业绿色发展效率均小于1,未达到DEA有效。三大区域工业绿色发展效率值排名依次为苏南>苏北>苏中,与未考虑期望产出的传统工业发展效率排名未保持一致。苏州地区的工业绿色发展效率除了2015年(1.104)之外,其他年份的工业绿色发展效率均值都小于1,说明苏州地区在工业节能减排方面面临着压力仍然较大。2013-2018年,考虑非期望产出的江苏省工业绿色发展效率与未考虑非期望产出的传统工业发展效率总体体现出较为一致变动趋势特征,但是二者在取值上体现出较为明显的差异。除了2018年以外,不考虑非期望产出的工业经济发展效率均高于江苏省考虑非期望产出的工业绿色发展效率,平均高出了0.029。苏南地区高出了0.014 2。这说明不考虑环境约束工业发展效率在一定程度上会高估了工业经济发展的实际水平,不能充分反映高质量发展要求下工业经济发展的质量水平。在工业经济发展过程中只有推动资源高效利用,加强工业环境污染治理,推动工业绿色转型才能实现江苏省工业经济可持续发展。

根据基于方向性距离函数的Malmquist-Luenberger模型即前述模型(3)和模型(4)。利用MAXDEA8.0PRO软件对江苏省及其各市工业全要素生产率与分解指数项进行测算,结果如表3和表4。

表3 2014-2018 年江苏省平均全要素生产率及其分解

表4 2014-2018 年江苏省各地区工业平均绿色全要素生产率及其分解

图3 2014-2018年江苏省工业ML生产率指数

图4 2014-2018年江苏省工业技术进步指数

图5 2014-2018年江苏省工业技术效率变化指数

图6 2014-2018年江苏省工业纯技术效率变化指数

(1)工业绿色全要素生产率指数(GTFPCH)分析。由表3和图3可知,未考虑环境约束的工业全要素生产率指数(TFPCH)除2016年(0.994)之外,其他年度工业全要素生产率均大于1,5年均值为1.081,说明江苏省工业全要素生产率五年平均增长了8.1%,这主要是由于江苏省工业技术进步6.0%和规模效应提升4.6%共同作用所致,而工业纯技术效率下降2.5%限制了工业全要生产率的有效提升。而考虑环境约束的江苏省各年工业绿色全要素生产率指数(GTFPCH)均小于1,均值为0.955,说明考虑环境约束的工业绿色全要素生产率平均下降了4.5%,这主要是由于受到工业绿色技术效率(GEFFCH)下降8.2%的影响,而工业绿色技术进步增加了4.0%能对江苏省工业绿色全要素生产率的提升起到一定的促进作用。进一步分析可知,工业纯技术效率(GPECH)下降8.4%是造成工业绿色技术效率下降的主要原因,而绿色规模效应(GSECH)提升0.2%对工业绿色全要素生产率的下降起到一定的限制作用。因此江苏省在未来应该在合理确定工业资源投入、优化工业资源配置的同时,重点加强在工业科技方面的自主创新,加大科技尤其是绿色工业技术的创新投入与内部管理创新,推动江苏省工业绿色技术效率的提升。2014-2018年江苏省工业GTFPCH均低于TFPCH,且二者呈现出较为一致的变动趋势即以2016年作为拐点呈现“先下降后上升”的趋势,从平均值来看平均相差-0.126,这说明非期望产出会造成工业全要素生产率一定的缺失,碳排放等工业污染产出会影响着工业GTFPCH的提升。

(2)工业绿色技术进步指数分析(GTECH)。由表3和图4可以看出,江苏省工业技术进步指数(TECH)和工业绿色技术进步指数(GTECH)是能够对江苏省TFPCH和GTFPCH产生正向促进作用的重要因素,二者在2014-2017年水平相差不大,而2018年GTECH却比TECH小0.087,差距相对较大,因此未来要特别注重进一步推动工业绿色生产和清洁生产技术创新。从整体上来看2014-2018年GTECH要比TECH小0.020。5年江苏省GTECH均值为1.040,说明江苏省2013-2018年工业绿色技术水平平均增长了4.0%,江苏省整个工业环境生产技术前沿面向前发生了显著移动,成为推动绿色全要素生产率提升的重要因素。

(3)工业绿色技术效率变化(GEFFCH)分析。由表3和图5可以看出,江苏省2014-2018年不考虑环境约束的工业技术效率变化指数(EFFCH)与考虑环境约束的工业绿色技术效率变化指数(GEFFCH)具有相同的变动趋势,整体上来看具有明显的下降趋势,EFFCH和GEFFCH最大值都是在2014年分别是1.115和0.967,最小值都是在2018年分别是0.902和0.854。江苏省2014-2018年未考虑环境约束的传统工业技术效率变动指数要比考虑环境约束的工业绿色技术效率变化指数大,平均值来看两者相差0.102。纯技术效率变动指数(PECH)和纯技术效率绿色变动指数(GPECH)两者在2014-2018年呈现出较为一致的变动方向,与EFFCH和GEFFCH两个指标的变动趋势具有较强的相似性,表明PECH和GPECH分别是影响EFFCH和GEFFCH变化的重要驱动因素。2014-2018年江苏省工业绿色纯技术效率变动指数均明显低于其传统的工业纯技术效率变动指数,二者均值相差0.059,这表明工业纯技术效率由于受到非期望产出的影响有所缺失。考虑环境约束的江苏省工业GEFFCH取值为0.895～0.976,其平均值为0.918,表明江苏省工业绿色技术效率平均下降了8.2%,进一步分析可知造成GEFFCH下降的主要原因是江苏省工业GPECH平均下降了8.4%,而江苏省工业绿色规模效应(GSECH)除2018年(0.974)之外,其他年份都大于1,平均值为1.002,表明总体来看江苏省工业经济绿色规模效应有所提升,对工业绿色技术效率和工业绿色全要素生产率的提升具有重要的促进效应。以上分析说明,江苏省工业经济在发展过程中仍然对资源规模投入依赖现象仍然较强,传统的粗放型工业发展模式尚未得以完全改变,对工业技术尤其是绿色生产技术的创新和有效使用仍然需要进一步加强。应该在合理配置工业经济投入要素,推动工业资源高效和循环利用的同时,加强工业企业内部流程创新与改造,坚持以工业前沿技术引领企业转型发展,培育和壮大战略性性产业和高新技术产业。

(4)由表4可以看出,江苏省辖市(13个市)2014-2018年工业绿色全要素生产率及其分解指标水平情况。考虑环境约束的江苏省工业绿色全要素生产率指数(GTFPCH)排名前四的依次分别是南京、常州、苏州和镇江,其工业GTFPCH大于1,说明这4个地区的工业绿色全要素生产率在2014-2018年平均来看有所提升,这与苏南地区经济发展水平较高、工业资本丰富、工业技术创新与利用水平高密切相关。其中南京工业GTFPCH处于省内最高水平为1.137,这主要是由于南京工业技术进步(GTECH)和工业绿色技术效率变化指数(GEFFCH)提升共同作用引起的。导致GEFFCH提升的主要原因是工业绿色纯技术效率(GPECH)水平的提升。江苏省其他地区的工业GTFPCH处于0.874～0.995,取值均小于1,处于这说明江苏省大部分地区考虑环境约束的工业绿色全要素生产率在2014-2018年均有不同程度的下降。淮安、泰州、宿迁、盐城和徐州是江苏省内工业绿色全要素生产率排名靠后的5个地区,其中4个地区为苏北地区,这5个地区的各年工业GTECH和GEFFCH均小于1是导致这5个地区工业GTFPCH小于1的两个重要因素。纯技术效率变动指数(PECH)较低是导致这5个地区工业绿色技术效率下降的主要因素,而规模效应变动指数(SECH)上升对这5个地区的工业绿色全要素生产率的下降起到一定的限制作用,也说明这5个地区工业GTFPCH对工业规模技术变动依赖性较强。

江苏省三大工业绿色全要素生产率(GTFPCH)平均值大小排序为苏南>苏中>苏南,这与三大区域经济发展水平和科技创新水平情况较为相符。苏南地区工业GTFPCH平均增长5%,工业GTECH平均增长3.7%,工业GEFFCH平均增长1.3%,工业GPECH平均增长4.1%,工业GTFPCH平均增长5%, 表明苏南地区工业绿色全要素生产率有所提升,这主要是得益于长三角经济带辐射效应,工业资本和科技创新水平较高,向低污染低能耗战略新兴产业转型效果较好。苏中地区工业虽然GTECH平均增长2.3%,工业GSECH平均增长4%,但是由于工业GPECH下降7.6%导致GEFFCH小于1,进而造成工业GTFPCH平均下降1.9%,说明苏中地区科技技术进步和规模效应提升对工业GTFPCH水平的提升具有显著的促进效应,但是工业GPECH对工业生产率提升的推动作用明显不足。苏北地区工业GTECH下降2.5%,工业GPECH下降8.2%,工业GSECH提升3.0%,工业GTFPCH 下降7.9%,这说明苏北地区工业绿色全要素生产率下降的主要原因是工业技术创新贡献不足,对工业前沿技术的追赶效应不够。苏北地区工业经济增长目前仍然是靠工业规模效应的拉动。可见,江苏省省内工业经济发展失衡, 总体上来说,苏北地区工业经济相对较为落后,工业经济增长动能和活力不足,工业生产效率相对较低。因此,未来应该统筹规划,推动区域合作,合理调整和优化工业资源投入,坚持工业技术进步与绿色技术效率提升双重驱动。